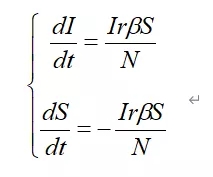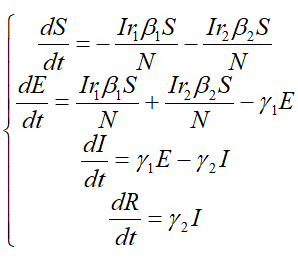疫况传播模型并非属于数学游戏范畴,它与封控举措启动的时间直接相关联,它还同医疗资源调配的时间有着直接联系。倘若能够看懂这些模型,那么你便能够理解为何专家们每日都围绕那些数字展开争论。
最简单的SI模型暴露了病毒传播的可怕速度
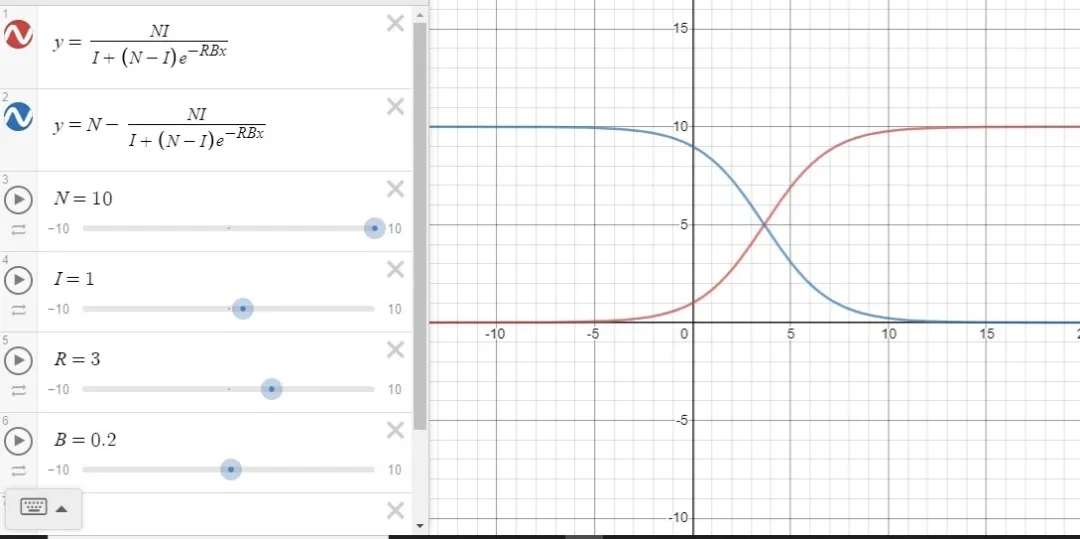
把人群以简单方式分成两类的SI模型,分别是健康人以及病人,假设总共存在10个人,其中1个病人每天会接触3个人,并且每次接触时有着20%的概率去传染对方,运用这个模型来开展模拟,仅仅在差不多20天的时间左右,全部10个人都会被感染。
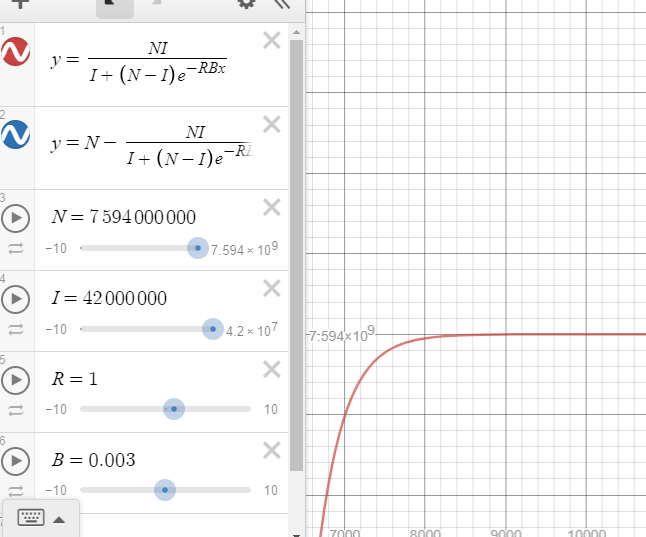
将此模型放大至现实世界,假定全球有着76亿人口,当下存在4200万艾滋病感染者,其中每人每日仅接触1个人,依据SI模型来进行计算,大概需要27年,全球每一个人都会感染艾滋病,这一结果尽管并不精准,然而直观地展现出传染病不加控制时的可怕后果。
SIS模型告诉你为什么有些病永远治不完
存在一些疾病,在被治愈之后并不会产生抗体,如此一来,人便会在健康以及生病的这两种状态之间来回地进行切换,而这就是所谓的SIS模型。比如说普通感冒这种疾病,对于一个人来讲,今年患上了,到了明年的话依然有可能再次患上,这是由于病毒变异速度较快或者是自身的免疫力并不持久所导致的。
于SIS模型里头,病人会凭借一定概率康复化身为健康人,而健康人是以一定概率再度被传染。要是康复速率赶不上感染速率,这般病症便会于人群中间始终存有,演变成地方性流行病,决然不会自行消逝。
SIR模型解释了为什么有些病得一次就终身免疫
例如腮腺炎、麻疹之类的病症,在感染并康复之后,身体当中就会生成抗体,进而再也不会患上第二次。SIR模型以SI为前提增添了康复者群体,这些个体被从传播链条里移除出去,不再参与到感染历程当中。
典型例子是2003年的SARS,它于2002年11月出现第一例,到2003年7月全球不再有新增,前后仅用8个月,由于感染过的人皆产生了抗体,病毒寻觅不到新宿主,故而在人群里消失了。
SEIR模型还原了新冠肺炎的真实传播过程
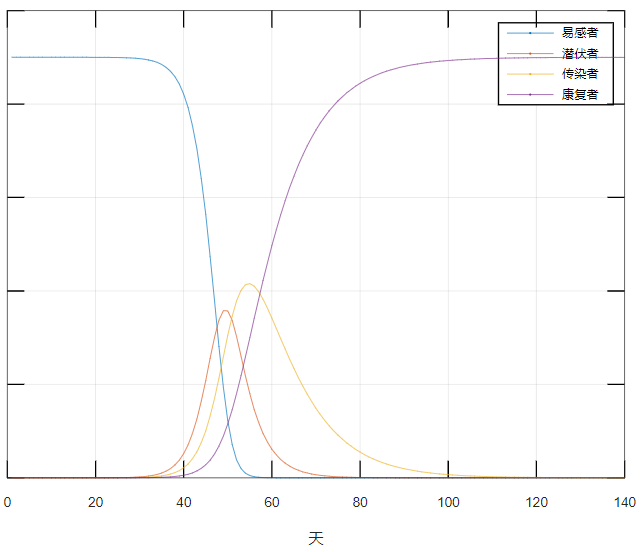
新冠肺炎存在潜伏期,处于潜伏期的人具备传染他人的能力,这便需求SEIR模型,该模型将人群划分成易感者、潜伏者、感染者以及康复者这四类,依据卫健委所提供的数据,潜伏期平均时长为5.2天,康复期平均时长是14天。
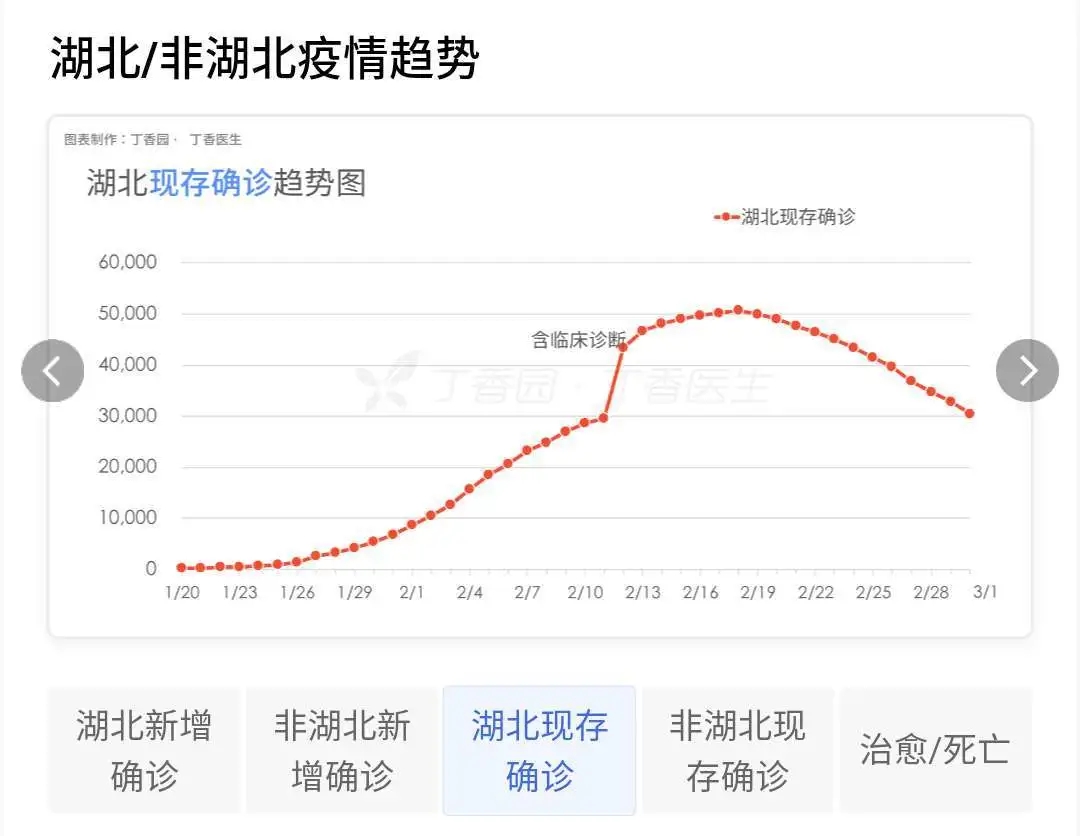
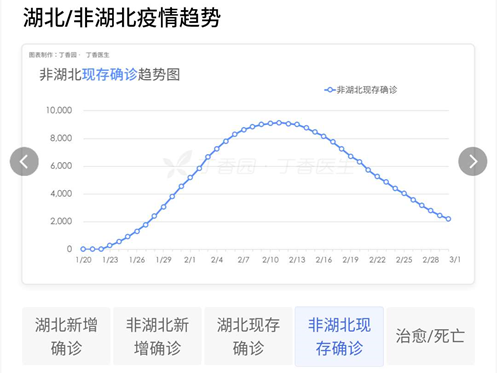
使用此模型来针对武汉疫情予以模拟,在12月8日的时候出现了第一例,于1月7日开始进行大规模传播,到1月31日感染人数抵达顶峰,在3月27日左右疫情基本上宣告结束。这样的时间线跟实际情形基本相吻合,证实数学模型的确是能够预测疫情走向的。
封城措施如何改变模型中的关键变量
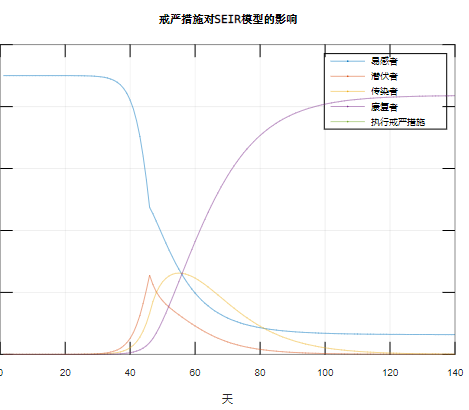
1月23日,武汉实施封城举措之后,所有的人都相应减少了出行的频次,并且陆续戴上了口罩。于模型当中,这所蕴含的意思便是,每一个人在每日所接触的人数由原来的3人下降到了1.5人,而传染的概率从原本的20%降低到了10%。将这两个参数进行改变之后,模拟曲线马上就发生了变化。
模型呈现出这样的情况,封城之后的二十天属于控制疫情的关键重要的黄金窗口期,如果于这段时间之内能够将传染数降低到一以下,那么疫情便会开始逐渐消退,而这个二十天时期的窗口期,是数学模型为决策者划分出来的生死界限。
加入死亡率的SEIRD模型更贴近现实
新冠肺炎存在着使约4.5%的个体面临死亡风险的情况,鉴于此,便有必要构建SEIRD模型,该模型是在SEIR模型的基础之上,增添了针对死亡者群体的考量。在这个模型里,康复概率所处比例为95.5%,死亡概率所占比例是4.5%,并且其他相关参数维持不变。
运用这个模型能够对医疗资源需求予以预测,即预测何时重症病人数量最为众多,预测需要多少张床位,预测呼吸机是否够用。这些数据直接决定着医院能否承受住疫情高峰,还解释了建造方舱医院的缘由,也解释了征用酒店的缘由。
读完这篇文章后,你认为要是在2019年末便运用这些模型去预测疫情的发展趋向,那我们所采取的应对举措会不会更早且更精准呢?欢迎于评论区域分享你的观点,点赞以使更多人能够理解这些数学模型。